Algorithmic Time and Space Complexities (Big O)
When diving back into programming and thinking about my future as a developer and engineer, I was reminded by other career developers that employers value candidates who understand the fundamentals of algorithms and data structures. A key aspect of this understanding is evaluating an algorithm’s performance in terms of "time" and "space" complexity. I used quotation marks to highlight that time and space are abstract. Actual execution time of an algorithm can vary greatly based on hardware, compilers, and other factors. However, time and space complexity measurements focus on how an algorithm scales as input size increases. This is where Big O notation comes in, providing a standardized way to describe an algorithm’s efficiency.
Linear Complexity O(n)
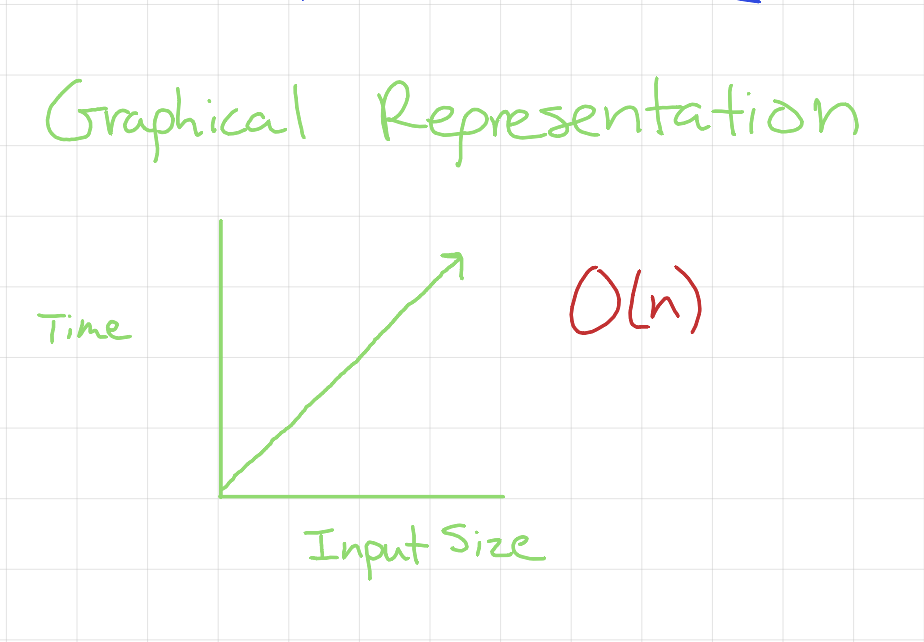
Linear Time
Say you are hosting an event with a sign-up sheet. Each person who attends is required to write down their name for attendance purposes. If your algorithm was to go through this list and read every name, you would be performing a linear time operation. To translate this into Swift code, imagine the sign-up sheet as an array. Instead of reading the names aloud, we'll use print statements as the equivalent operation:
func printNames(names: [String]) {
for name in names {
print(name)
}
}
We say this algorithm operates at O(n) time complexity because as the number of attendees increases, the time required to read the list increases proportionally. In other words, as the input size grows, the time to complete the operation scales linearly. In Big O notation, we sometimes write this as c × O(n), where c represents constant-time operations like reading a name (print(name)) and accessing the next element (array indexing). However, we drop c in Big O notation because constant factors become negligible as input size grows, so it becomes O(n).
Linear Space
Now, imagine you need to make a copy of the sign-up sheet to share with a co-host. Instead of making attendees write their names twice, you manually copy each name to a new sheet. This is an example of linear space complexity. Here’s how this translates into Swift code:
func copyNames(names: [String]) -> [String] {
let copy: [String] = []
for name in names {
copy.append(name)
}
return copy
}
The key takeaway is that the new array (copy) directly corresponds to the size of the input array. As the input size increases, so does the memory usage. We express this space complexity as O(n).
Quadratic Complexity O(n²)
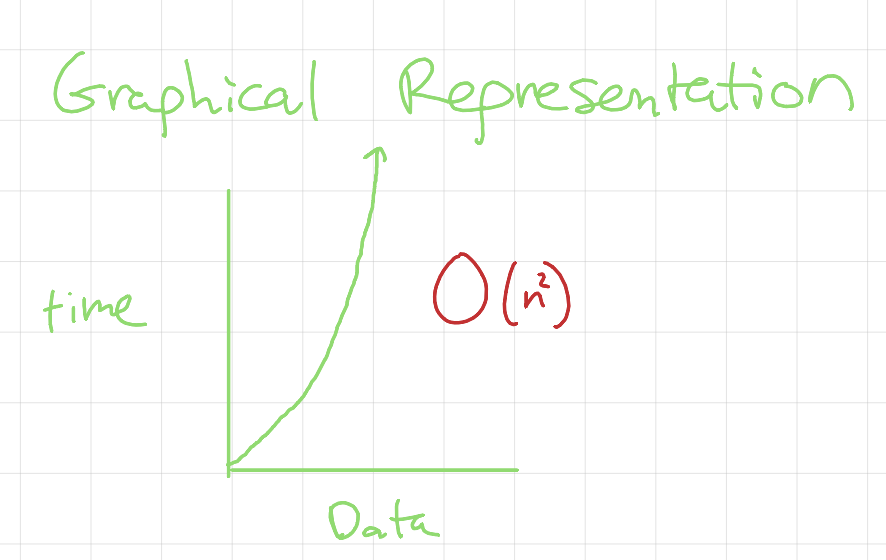
Quadratic Time
Since we've used the sign-up sheet example to its full extent, let's try something new. Suppose you’re making a grocery list from multiple recipes, but you don’t want duplicate ingredients. As you write down each ingredient, you first check if it’s already on the list. If it’s not, you add it. This results in O(n²) complexity. In Swift, we can express this as:
func createGroceryList(recipes: [String]) -> [String] {
var groceryList: [String] = []
for ingredient in recipes { // O(n) operation
if !groceryList.contains(ingredient) { // O(n) operation
groceryList.append(ingredient)
}
}
return groceryList
}
Here’s why this is O(n²): The outer loop runs O(n) times, iterating over each ingredient. The .contains() function also runs O(n) times in the worst case because it searches through the entire groceryList. Multiplying these together gives us O(n × n) = O(n²). As input size grows, execution time increases quadratically.
Logarithmic Complexity O(log n)
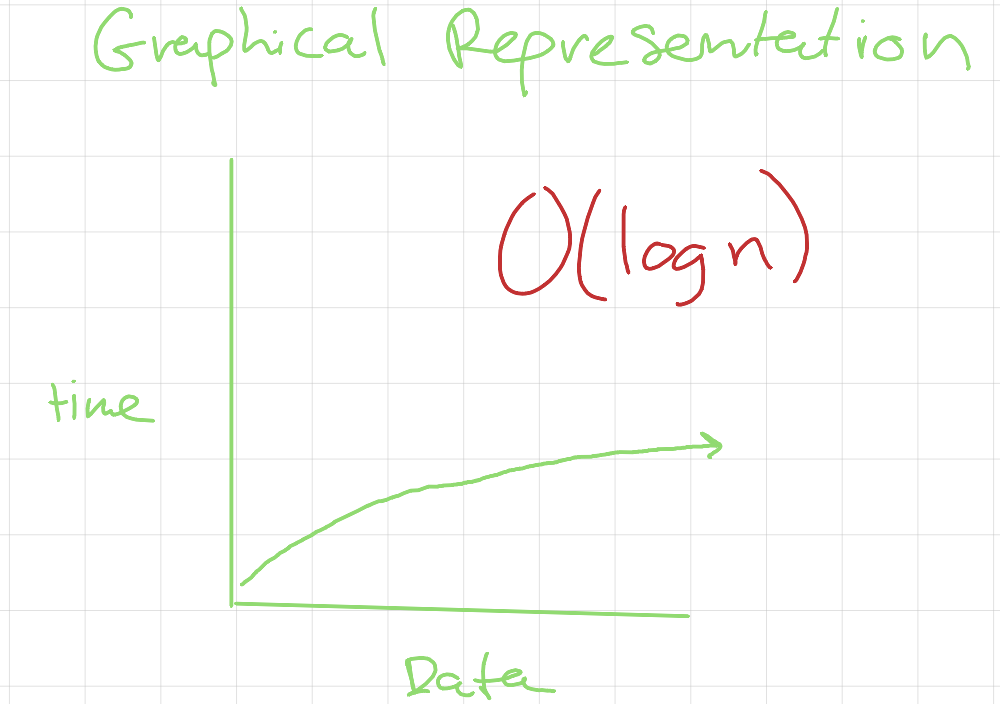
Logarithmic Time
Logarithmic complexity occurs when an algorithm progressively reduces the problem size instead of examining every element. A classic example is searching for a value in a sorted array using binary search. Imagine our grocery list is alphabetically sorted. Instead of scanning every ingredient, we can cut the list in half each time we check a value. Here’s an example:
func findIngredient(ingredientToFind: String, sortedGroceryList: [String]) -> Bool {
let midpoint = sortedGroceryList.count / 2
if ingredientToFind <= sortedGroceryList[midpoint] {
for index in 0...midpoint {
if sortedGroceryList[index] == ingredientToFind {
return true
}
}
} else {
for index in midpoint..<sortedGroceryList.count {
if sortedGroceryList[index] == ingredientToFind {
return true
}
}
}
return false
}
This algorithm splits the search space in half, significantly reducing the number of elements we need to examine. Every time we halve the input size, we take O(log n) steps to find an element. This logarithmic growth results in an asymptotic curve, as illustrated in graphical representation above.
Tags: tech, data_structures_algorithms